本文长期更新,记录力扣碰到的一些趣题
我的力扣主页
动态规划
多边形三角剖分的最低得分
题目大意
给你一个凸 $n$ 边形,要你把它全部分成三角形,每个三角形的得分为三个顶点数字的乘积,求该图形最低总得分
例子:下图的最低总得分即为13
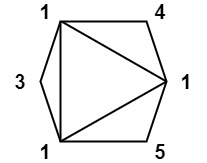
思路
这题虽然不难,但是转换还是挺巧妙的,将图形的一条边当作区间DP中的区间,边左右侧的图形又形成新的图形继续分割。选取分割点,就是给一条边已有的两个点选剩下的一个点组成三角形,再加上左右图形的得分就是选取当前分割点的总得分,那么DP使其最小即可。这里选用记忆化搜索形式来写,代码更加简单。
class Solution:
def minScoreTriangulation(self, v: List[int]) -> int:
@cache
def dfs(l, r):
if l + 1 == r: return 0
return min(v[l] * v[r] * v[i] + dfs(l, i) + dfs(i, r) for i in range(l + 1, r))
return dfs(0, len(v) - 1)数据结构
子数组中占绝大多数的元素
题目大意
给定一个数组,每次查询数组某个区间出现 threshold 次数或次数以上的元素,保证 threshold 大于区间长度的一半。
区间长度与查询次数都是 $10^4$ 的量级
思路
用数据结构的话,直接权值线段树维护 + 摩尔投票就好了。但这么无趣的做法,肯定上不了这篇博客。
反过来思考,如果该区间存在一个数出现次数大于等于 threshold ,那么我们在该区间随便选一个数,是目标数的概率大于 50%,这是多么高的概率!
因此可以直接随机化选数一定次数,每次通过二分判断该数在当前区间出现次数是否大于 threshold 。如果满足直接返回。如果随机化选取结束后还没有,就假定不存在这样的数。
参考🍓大佬
class MajorityChecker:
def __init__(self, arr: List[int]):
self.arr = arr
self.indexes = defaultdict(list)
for i, num in enumerate(arr):
self.indexes[num].append(i)
def query(self, left: int, right: int, threshold: int) -> int:
ROUND = 20
for _ in range(ROUND):
index = randint(left, right)
num = self.arr[index]
count = bisect_right(self.indexes[num], right) - bisect_left(self.indexes[num], left)
if count >= threshold: return num
return -1


