C++浮点数问题

今天下午遇到这样一道题，被卡了精度，联想起以前比赛时被卡精度的题，以及计算计组成原理的IEEE浮点数标准。故在此进行总结

数据类型

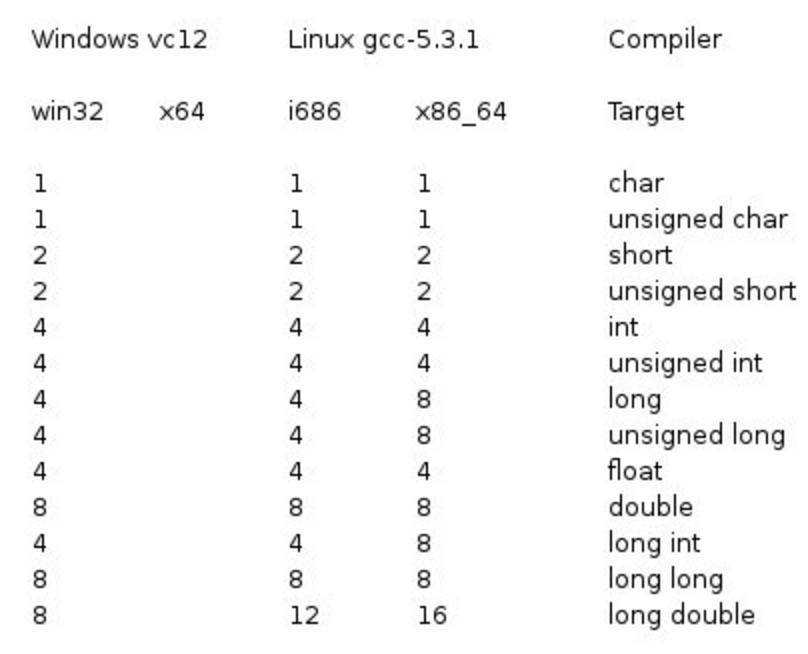
在不同的计算机，不同的编译器中，常用的 int, double, long long 类型存储大小基本不变，但是 long double 变化却很多，可偏偏这种数据类型在卡精度时又很常用，所以有必要好好分析一下。

在C的标准中，仅规定 long double 的精度范围大于等于 double

在 msvc（即VS使用的编译器）中， long double 等同于 double ，都是8个字节

Thelong double type is identical to the double type.

而在 gcc 中两者是不同的

32位下long double 是12个字节, 64位下是16个字节.

现今竞赛环境多为64位机 G++/GCC，即 long double 占用了16个字节，128位。

然而实际编译时，由于x86架构上 fpu 的存在，大部分编译器将 long double 编译成80位的浮点数，用科学计数法的话，其尾数部分是64位。剩下的部分主要用于内存对齐，防止存取的麻烦以及内存空间碎片化。

也就是说，尾数部分刚好存得下一个 long long ，不会损失精度。

然而，double 尾数部分就没有那么大了

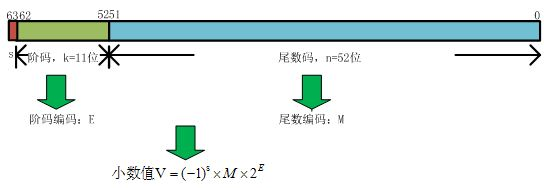
所以 long long 在转为 double 时会损失不少精度

库函数

想起以前很多时候，觉得一个库函数好用就天天拿来玩，却没有去想其功能与使用范围。导致埋下了不少坑。

sqrt

就我个人而言，最易出问题的当数 sqrt 函数

很多人都知道这个函数是求一个数的根，但是却没有去看其返回类型以及传入类型

查看cmath库的定义源码

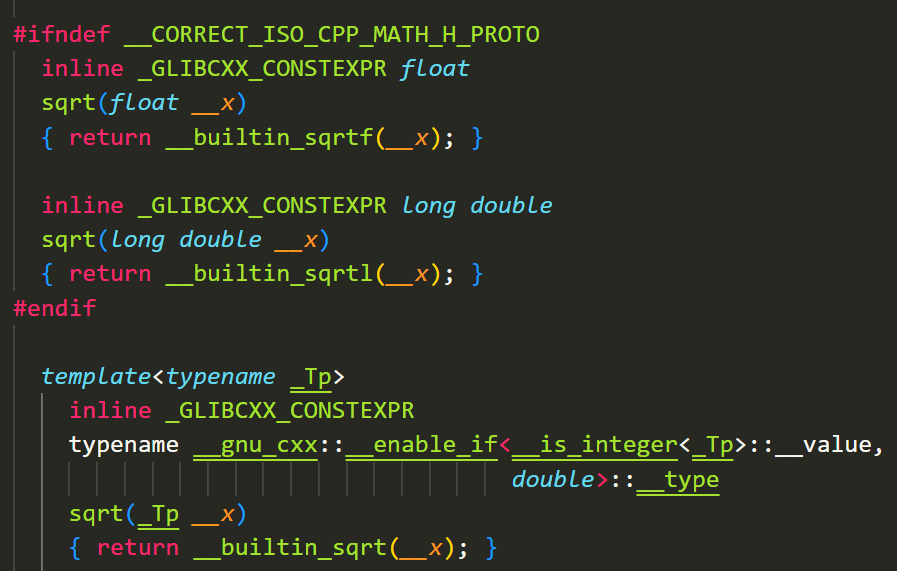
可见除 float，long double类型外，其余均返回 double

其中

float 另调用 math.h 的 sqrtf 函数

long double 另调用 math.h 的 sqrtl 函数

其他类型则调用 math.h 的 sqrt 函数

该函数在C库仅有如下声明

故整型均会强转为 double 进行运算，long long 便是在此处传入时损失了精度。若想不损失精度，要么传入的时候强转为long double ，要么调用C库的 sqrtl 函数。

其他函数

后续又对许多数学库函数进行了观察，发现很多库函数都对 float ,long double 进行了单独处理，对于 float 函数名基本都为常见的那个后面加个f，对于 float 函数名基本都为常见的那个后面加个l。数学库的函数大部分都是返回 double 型，而非整型。初学者往往会将 pow，ceil 误当作返回整型的函数，一定要注意精度的损失。

顺带一提，这些数学库函数的复杂度基本都是可以当作 $O(1)$ 的，只是常数比较大，其底层有用到类似牛顿迭代法一类的数学加速方法。

算法上避免精度误差

避免除法取根号等运算，不仅可以在精度上提升，还可以提快速度。我曾经就有因为除法而在一道题上超时。

替换方法举例：

如将

for(int i = 1; i <= sqrt(n); ++i)

替换为

for(int i = 1; i * i <= n; ++i)

将

int p2(int x) {
    return x * x;
}
double dis(int ax, int ay, int bx, int by) {
    return sqrt(p2(ax - ay) + p2(bx - by));
}

替换为

int dis(int ax, int ay, int bx, int by) {
    return p2(ax - ay) + p2(bx - by);
}

并直接使用整数比较距离远近，只在结果输出时对其进行特殊处理。